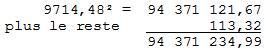Algorithme de calcul de racine carrée

Calculer une racine carrée à la main

Calculer une racine carrée à la main

1995

Pendant mon adolescence, mon grand père m'a appris à "extraire une racine carrée à la main", il s'agit de la méthode manuelle pour calculer une racine carrée sans calculatrice !

Vous allez me rétorquer que cela ne sert à rien ! Et bien c'est vrai ! Sauf si vous voulez par exemple implémenter vous-même cet algorithme (car au final, c'est un algorithme)...

Et même si ça ne vous intéresse pas à implémenter, au moins vous pourrez, en retenant la méthode, vous dire "je sais le faire" ;)

Anecdote : cette méthode m'a servi en 1997 pendant que je passais le concours FESIC d'entrée aux grandes écoles... pas de calculettes autorisée, donc j'ai utilisé cette méthode pour valider un de mes résultats...

La méthode

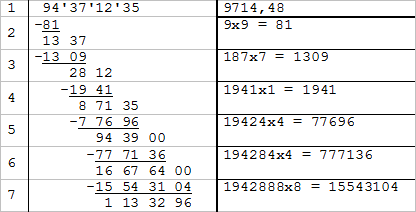
  1. Séparer en tranches de deux chiffres le nombre de départ en partant de la droite.
  2. Quel est le plus grand carré obtenu dans 94 ? : 9 x 9 = 81.
    Je déduis 81 de 94 et j'abaisse la tranche suivante.
    9 est le premier chiffre de la racine.
  3. Je double la racine, je laisse le chiffre de droite (7).
    Combien de fois 18 est contenu dans 133 ? (réponse = 7).
    187 x 7 = 1309.
    Je déduis 1 309 de 1 337 et j'abaisse la tranche suivante.
    7 est le deuxième chiffre de la racine.
  4. Je double la racine, je laisse le chiffre de droite (2).
    Combien de fois 194 est contenu dans 281 ? (réponse = 1).
    1 941 x 1 = 1 941.
    Je déduis 1 941 de 2 812 et j'abaisse la tranche suivante.
    1 est le troisième chiffre de la racine.
  5. Je double la racine, je laisse le chiffre de droite (5).
    Combien de fois 1 942 est contenu dans 8 713 ? (réponse = 4).
    1 942 x 4 = 77 696.
    Je déduis 77 696 de 87 135 et j'abaisse la tranche suivante qui ne peut être que des zéros et je met une virgule à la racine après le quatrième chiffre de le racine (4).
  6. Je double la racine, je laisse le chiffre de droite (0).
    Combien de fois 19 428 est contenu dans 94 390 ? (réponse = 4).
    194 284 x 4 = 777 136.
    Je déduis 777 136 de 943 900 et j'abaisse la tranche suivante.
    4 est la première décimale de la racine.
  7. Je double la racine, je laisse le chiffre de droite (0).
    Combien de fois 194 288 est contenu dans 1 667 640 ? (réponse = 8).
    1 942 888 x 8 = 15 543 104.
  8. Je déduis 15 543 104 de 16 676 400 et j'abaisse la tranche suivante.
    8 est la deuxième décimale de la racine.

La preuve :